秋田09時観測の高層データを2回取り上げました。簡単に紹介すると
空気1㎥当りのエネルギー=エネルギー密度を導入しました。
結果、冷夏と猛暑のエネルギー密度が成層圏まで、同じだけ低かったり、高かったりしました。
7、8月の高度15000mは地上付近に比べ質量(エネルギー?)密度が125/1000=25/200=5/40=1/8程度です。
それが、同じだけ変化するには何か理由があるはずです。
複雑に思えた温度の高度分布も温位にすると2本の直線でほぼ近似できました。
しかし、気圧の分散が奇妙な分布をみせ、分散が小さくなる高さ付近で、等温度層や等温位層が出現するのをみました。
今回は気団の入れ替わりのない南極にある昭和基地の高層データ(09)を再び見ていきます。南極については繰り返しになる部分もありますがご容赦願います。
1.南極のイメージと使用データ
南極は一年中他より気温が低く上空に空気が流れ込み地上で気圧が高くなり周辺に吹き出し、気団の入れ替えはないイメージがあります。(私だけかもしれませんが・・)
てっとり早くイメージを知りたいかたは3.大気大循環の「大気圏の温度分布」の
を参照してください。
データは気象庁のホームページからダウンロードした
1989~2010年の09時観測の資料です。
現地時間では午前3時の明け方前に観測されたデータです。
なお、気温は絶対温度表示にします。
高さ毎の質量密度を求め気圧を確かめたいからです。
2.高度別の気温と気圧別の気温
気温の分布は上図のように気圧と高度を軸にして示される概念図が一般的だと思います。
平均を示したグラフはなかなかみられません。
まず、実際に南極の高度別と気圧別の気温平均値(今後こうしたものを平年値と呼びます)を見ておきます。
高度対気温
気温は見てのとおり15000m付近に特徴があります。
15000mの特徴は温位の飛び(不連続)であることが分かります。
直線は1月の温位の傾きですが、南極は秋田のように数本の直線で各月の温位を近似できませんでした。
高度別の温度と温位グラフはWithPhot「南極昭和基地温度と温位」を参照してください。
次のグラフは9~12月の気温のグラフです。
真冬の8月から気温が上がって行く過程15000m付近で温度の飛び=不連続が発生しています。
なんか訳の分からない変化ですが・・・・
しかし、このブログでたびたび空気は混ざりにくい変わった性質をもった気体であること指摘しました。
そうした性質を考えれば、安定な成層状態をしている大気では、ちょっとした大気の入れ替えで気温や温位の飛びは頻繁に起こるはずです。(水平方向で起こっているのが前線です。)・・・?南極では大気の入れ替えは考えにくいのですが・・?
とにかく観測事実を見ていきます。
気圧対温度
10hPa以下のデータは解釈ができないので、切ってしまおうかとおもったのですがデータ数が多く真実のようです。一年を平均したものですから特定な月や現象のものかもしれません。・・・あるいは、10hPa以下の空気と以上の空気とでは性質が違う・・
高度15000mのように特定の気圧面で温度の飛びはみられません。
どうでしょうか?気温の飛びを除き、分布は高度分布に似ているように思えます。
温位を気圧別に見てみましょう。
高度による温位より綺麗な分布に見えます。
等温位層がありそうですが、これは年間の平年値ですので大気を特徴付ける層かも知れません。
すこし気になるので月毎の様子もざっとみましょう。
日照の多い1~3月はほとんど変わりません。
1月は夏で7月は冬です。
同一気圧面では夏に温位高く冬に低い傾向は下層より上層のほうがハッキリしています。
ここでの上層、下層は温位の傾きの違いで分けています。
高度による温位と比べてみましょう。
10hPaの年平均高度は30000m程度です。
10hPaの変動は100k程度なのに、30000mの変動は50k程度です。
上の図は、高さ毎の気圧分散の移動平均ですが高さ毎の気圧分散として見て下さい。
15000m付近には気圧の飛び(?)もあるのかもしれません。
いずれにしても、高度別に気温と気圧を調べる必要がありそうです。
***
***
3.空気の質量密度と気圧差
実は高度別に気温と気圧を調べるとは、高度毎の1㎥あたりの質量=質量密度を調べることに他なりません。
高さごとに1㎥あたりの質量を積み上げればそれは気圧差になります。
そうしたことを少し説明させてください。
内容は質量密度から気圧差を求める物理です。
常識的なことなのですが気温と気圧から空気の質量密度が計算できます。
しかし、ここから気圧差を計算するのは単位を揃えなければならず結構面度です。
地上付近は100mの丘に登ると約12hPa気圧が下がりますが、これを例に計算してみます。。
空気を理想気体とみなします。
nモルの空気があれば
PV=nRT
が成り立ちます。
その体積は V=nRT/P (㎥)になります。
です。
その質量Mは
M=0.029×n (kg/mol)(mol)
体積はV(㎥)ですから1㎥あたりの質量=質量密度は
ρ=M/V=0.029n/(nRT/P)=0.029P/RT
(kg/㎥)
となります。
ここまで、単純な作業ですが、かなり面倒な作業に私には思えます。
正直、これをnモルではなく1gの空気を考えて計算するなど正気のさたではないと思います。しかし、これに似た計算を気象は1gの空気で計算するのです。
なぜ面倒な計算をさらに面倒にして計算するのか理解に苦しみますが・・・
R=8.314 (J/mol k)
(私は8のあとの小数点以下は円周率の数字を並べると覚えました。)
ここまで書いても実際に質量密度を求めようとしてももやもやします。
1000hPa、0℃の空気の質量密度をもとめてみます。
(普通は1013hPa,20℃位で計算されていると思います。水蒸気は多くても3%程度ですから無視します。)
1000hPa=100000Pa=100000(N/㎡)=100000((J/m)/㎡)=100000(J/㎥ )
0℃=273.2k
です。
ρ=0.029×100000/(8.314×273.2) (kg/mol)(J/㎥)/((J/mol k)k)
= 1.28 (kg/㎥)
なるべくこうした考え方は避けた方がよいのですが、さすがに面倒なので1㎥の立方体を考えましょう。(底面積が1㎡なら円柱でも三角柱でもよい)
この立方体の空気が100m積み上がると質量は
M=ρ (kg/㎥)×100(㎥)=1.28 (kg/㎥) ×100(㎥)= 128kgです。
一番下にかかる力はMg=128×9.8 (kg)(m/sec sec)= 1254.4 (N)
立方体を考えていますから底面積は1㎡です。
1㎡に1254.4Nの力がかかることになります。
1㎡当たりにかかる力が圧力ですから
⊿P=1254.5 (N/㎡)=1254.5 (Pa)=12.545 (hPa)
地上付近の気圧は1000hPaくらいですから、この結果は地上付近では標高100mの丘に登ると約12hPa位気圧が下がることに対応しています。
質量密度ρ= 1.28 (kg/㎥)から、地上付近の高度差100mの気圧の差12hPaが分かりました。
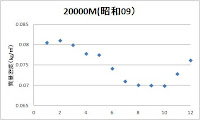
さてデータを整理した結果、南極では1月の高さ1000、1500、2000mの質量密度は1.14、1.08、1.02kgでした。
1000~2000mの平均質量密度は1.08kgとしてよいでしょう。
1000~2000mに底面積1㎡の空気の柱を考えると力の差は
1.08×9.8×1000 (kg)(m/sec sec)(m)=10584 (N)
これは1㎡にかかる力の差ですから圧力差になります。
⊿P1000-2000(理論)=10584 (N/㎡) =10584 (Pa)=105.84 (hPa)
となります。
こうした値を以下理論値と呼びます。
実際の気圧差は1000m 868.6hPa、2000m 762.1hPaで
⊿P1000-2000(観測)=106.5 (hPa)
でした。
こうした値を以下観測値と呼びます。
観測値―理論値=106.5-105.8=0.7(hPa)
この差は誤差でしょうか?
理論値は、空気を理想気体として計算しています。
実際の空気は理論値より重いのでしょうか?
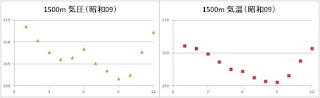
上図は昭和基地で観測された月毎の現地気圧と気温の平年値です。
データは気象庁のホームページから得ました。
南極のイメージからすると、冷たくなれば下降流が強まり気圧が高くなりそうですが・・
このような大雑把な感覚と実際のデータ違って気温の低い8月は気圧が低くなって気圧の極値(低)が3月と10月にあります。
それでは、高度別の気圧と気温を見ていきます。気温は質量密度も求めたいので絶対温度で記述しています。
日照のない6月に何故気圧が低くなるのか不思議ですが・・そのことはさておいて
質量密度は
ρ=M/V=0.029/(RT/P)=0.029P/RT
でした。
この質量密度が2000mまで続いていたとしたら1月と他の月の気圧差は広がるはずです。
地上気圧は3月より6月のほうが大きいのでどこかの高さで質量密度の逆転が起こっていると思われます。
10000mで3月と6月の質量密度の逆転が起きています。
次の高度5000mでは5~10月について気圧の相対的な関係はあまり変化がないと考えられますが・・
8月の質量密度が一番高いので次の高さ(3000m)では6月(495.3hPa)と8月(492.9hPa)の気圧差(2.4hPa)は小さくなるかもしれません。
また、1月(507.0hPa)との差(-11.7hPa)も小さくなるはずです。
気圧のレンジは同じとってあります。
1月(666.7hPa)との気圧差(-8.0hPa)は小さくなりました。
こちらは理屈通りです。
今回も1月の質量密度が小さく次(1500m)で1月と6月の気圧差は小さくなるはずです。
ここでも6月より8月の質量密度はほぼ同じ(すこし大きい)ですから次(1500m)気圧の差は広がらないはずです。
6月と10月の質量密度はやや10月のほうが小さいので次(1000m)でやや気圧差が開きそうです。また、3月の質量密度はかなり低く気圧差は大きくなりそうです。
次は地上の気圧のイメージ近づくと考えられます。
1000m
質量密度の分布は1500mと同じく次(500m)で気圧を地上気圧の平年値に近づけるイメージです。
500m
かなり気圧と気温は地上イメージに近くなりました。
これは高層観測で観測した平均値ですの地上の平年値ではないことに注意して下さい。
大雑把に気圧と質量密度の関係は良好に思えますが、3000メートルでは気圧差が小さくなると考えられたのに逆に大きくなるなどしました。
質量密度と気圧の関係をもう少し丁寧に見た方がよさそうです。
5気圧差と質量密度差
これから、各月の同高度の気圧差と質量密度差を比べていきます。
その前に簡単に気圧と密度の関係を振り返ります。
例えば、1月と6月の大気を考えます。
500hPaの高度が5000mと同じだったとします。
1月は夏で6月は初冬ですから、温度は1月のほうが高く、1月の質量密度1月は小さくなります。
密度1月は密度6月小さいとき、5000mより少し高い所で1月の気圧P1月と6月の気圧P6月とでは1月の気圧のほうが高くなります。
同じ高さ、圧力で
密度1月<密度6月 なら P1月>P6月 (5―1)
となります。
質量密度が小さいので黄色の薄い円盤の重さは青の円盤より軽くなります。
円盤の面積を1㎡とすればP1月の圧力は黄色の円盤のmg=密度1月×高さ×1㎡×gを引いたものになるからです。
ところで、1月と6月は同一の高さで気圧は違っているのが一般的です。
例えば高さ5000mで1月のほうが10hPaほど高かく、密度は前と同じで密度1月<密度6月と仮定します。
すると、気圧差は5100mでは開き、4900mでは接近することになります。
この関係をもとに、月毎の気圧差と密度差の関係をみたいのですが、全てを比べる訳にもいきません。
日が昇らない6月の地上気圧は前後の月より高くなっています。
8月は地上気温が10月は地上気圧が一番低くなっています。
6月の気圧と密度から8月と10月の値を引いて調べますが、まず、6月について、観測値と理論値を比べます。
ほとんど一致して重なり観測値が見えませんが、違いは当然あります。
0より大きい点は、乾燥空気より質量密度が大きいか水平方向から空気が流れ込んで質量密度が大きくなっていると思います。
0より小さい流域は質量密度が乾燥空気より小さくなることはあり得ませんから、空気が水平方向に吹き出していると思います。
このあたりはもっと慎重に考えなければいけないかもしれませんが、ここではこのように考えておきます。
また、角運動量の法則からこの領域では高さが低くなるにつれ地球の回転方向とは逆向きの風が吹きやすくなると思います。(コリオリ力とは角運動量保存則の見かたを少し変えただけです。)
5000m以下でプラスになっていますが、南極のイメージから周辺から空気が流れ込むとは考えにくいです。
消去法で乾燥空気より質量密度が大きくなっていると考えられます。
(他に可能性はあるでしょうか?今のところ思いつきません。)
上の図は実際の6月と10月の気圧の差です。
Aの領域は質量密度が6月のほうが大きいので、25000mでは気圧の差は小さくなるはずです。
A領域で10月は水平方向からの空気の流れ込みが強いか、乾燥空気の質量密度より大きい、あるいはその両方だと思います。
その他の高さでは地上付近での気圧差の広がりが足りませんが、傾向は概ね合っているようです。
6月-8月
Aは例えば6月と8月が30000mで同じ気圧だとすると、高度が低くなるにつれ6月の気圧が高くなり8月との気圧差が広がる領域です。
Bは逆です。
5000mで6月の気圧が8月より高かったとすると高度が低くなるとその差は小さくなる領域です。
実際の気圧差は
上の図は実際の6月と8月の気圧の差です。
Aの領域は質量密度が6月のほうが大きいので、25000mでは気圧の差は30000mより小さくなるはずです。
しかし、気圧差は変わりませんから、6月-10月と同じで水平方向からの空気の流れ込みが強いか、乾燥空気の質量密度より大きい、あるいはその両方だと思います。
Bには不思議な15000mの不思議な境界が現れています。
Cは気圧差が小さくなるはずの領域ですが、小さくなりません。
水平方向から空気が流れ込めば気圧差が変わらないと推論可能ですが、空気が流れ込むと考えるのは難しいです。
Cでは気圧差は変わりませんから、実際の質量密度は6月と8月で変わらないと言えそうです。
こうしたことからも6月の5000mまでの空気は乾燥空気の質量密度より高いことになります。
******************************
空気の質量密度と気圧の関係は入門時触れられた後はP座標近似一色となります。
しかし、今回のこうしたことを調べていなかったとしたら気象学者の怠慢だと思います。
位置エネルギーを無視した温位や相当温位では、温暖化など予想できる訳もありません。、台風の相当温位分布も不正確で、観測結果は安定な成層構造になってしまうのです。
(モデルは温暖化を予想できるのか? 参照)
ところで、温室効果理論は様々に変化して今も生き残っています。
「CO2が、赤外線を吸収し、振動して温度が上がる。」との説明は電子レンジで者を暖める説明のイイカゲンな引用です。
事の真偽は分かりませんが電子レンジは「水分子が振動し、その摩擦熱で温度が上がる。」とか言うものでした。
振動させるのはマイクロ波で物を暖めるエネルギー源は勿論電気です。
つまり、マイクロ波と赤外線の違いはありますが、
温室効果は電源無しに物を暖める魔法の電子レンジ
になってしまいます。
温室効果は電源無しに物を暖める魔法の電子レンジ
になってしまいます。
このように温室効果はエネルギー保存則を無視しているのです。
こんないい加減な説明をする御用環境学者は辞職すべきだと思います。
税金を使って、国民をだましている訳ですから・・・
このような馬鹿げた温室効果が生き残るのは
国の経済政策で原発が必要で、原発を正当化する為に温室効果が必要なのだと思います。
温室効果が必要なのは日本だけではないようです・・・
どこかの国の政治家が他国に国家としてのプライド云々と言っていましたが・・
この国は国家としてのプライドがあるのでしょうか?
CO2の振動の自由度について誤りがありました。
お詫びします。
しかしCO2より温度低い物質(空間)から放射された赤外線を吸収して温度が上がるとするのは明らかに第2法則に反する誤りです。
どこかの国の政治家が他国に国家としてのプライド云々と言っていましたが・・
この国は国家としてのプライドがあるのでしょうか?
CO2の振動の自由度について誤りがありました。
お詫びします。
しかしCO2より温度低い物質(空間)から放射された赤外線を吸収して温度が上がるとするのは明らかに第2法則に反する誤りです。
・・・他国では経済政策ではなく軍事政策でも温室効果が必要なのでしょう・・・
(信じられないと思いますが、ノーベル賞は御用学者の投票(推薦)で決まってしまう一面もあるのです。つまり、政策で温室効果が必要ならならノーベル賞はお金で買えるのです。事実、無責任な御用環境学者を使ってノーベル賞をお金で買ったと私は思います。)





































0 件のコメント:
コメントを投稿