ー第2法則を原理として書き直しましたー
空気の成分は窒素N2 78%、酸素O2 21%、アルゴンなどAr and etc. 1%です。
80kmの高さまで成分比はかわらないそうです。
これは、ここに10000個の空気粒子があるとすると、N2が7800個、 O2が2100 個、 残りのAr 等が100 個の割合になります。
CO2 はあるか無いかの3個です。.
大気圧を1000 hPaとすると、各成分の分圧は次のようになります。
N2:780hPa、O2:210hPa、Ar & etc.:10hPa。
ところで気象学では小さな原子量の原子など軽いと言っています。
そして、軽いガスは浮かび、重いガスは沈むと言います。
当然なことだと思われるでしょう。しかし、この考えは第2法則に反するのです。
第2法則によれば理想気体の混合ガスは勝手に分離しないことになります。.
0. 原子量の小さなガスが軽い訳
ここに3つの風船があります。
赤に酸素、青に窒素、ピンクには空気が詰められています。
詰められた粒子の数は同じです。
この風船が浮かぶかどうか考えると、答えは赤が沈み、青は浮かぶ、ピンクは浮きも沈みもしないと考えられます。
しかし、この答えには同温、同圧、同体積であることが前提になっています。
そのほかにも、例えば青の風船は窒素だけが集められ風船膜の内側に閉じ込められていなければなりません。
そうして、質量密度が小さくなって浮くのです。
第2法則はピンク風船の中で、窒素と酸素が勝手に分かれることを認めません。
しかし、実際の空気では分かれる現象が起こっています。
温暖前線や寒冷前線がそうです。
第2法則はこのように分かれている理由を説明するように要求します。
気象現象とは物理的に非常に不可解な現象なのです。
気象学者は聞く耳をもっていないようですが・・
1.
ギブスのパラドックス
部屋の中に小さな箱を考えます。箱と部屋は断熱材で出来ています。
箱と部屋は共に熱平衡に達しているとします。
部屋と箱を満たしているのは窒素とヘリウムです。
部屋と箱は次のようになっています。
1. 温度と圧力は部屋と箱の中は同じです。
2. しかし、窒素とヘリウムの分圧は違うとします。
箱のフタを開けるとどうようになると思いますか?
勿論、部屋と箱の中で、窒素と酸素の分圧が同じになります。
始めの分圧とは異なってしまいます。
温度と圧力が同じなのに変化が起こりました。
第2法則はこれを次のように言います。
フタが開けられてエントロピーが大きくなった。
箱の中かあるいは部屋のどちらかのエントロピーが小さくなった可能性はあります。
しかし、箱と部屋のエントロピーのトータルは大きくなります。
これが、ギブスのパラドックスと呼ばれるものです。
もう少し、ギブスのパラドックスを説明しましょう。
例えば仕切られた同じ大きさの箱があり、一方に窒素が詰められ、他方は真空とします。
A
もし、窒素と真空の箱の壁に穴をあると、窒素は自由膨張してエントロピーは大きくなります。
温度は窒素粒子の平均運動エネルギーに比例します。
運動エネルギーは変化しませんから、温度は変わりません。
体積は2倍になり、圧力は1/2になります。
エントロピーSからΔS増えたとしましょう。
面倒な計算をすれば、ΔSは求めることができますが、ここではそんなことはしません。
B
窒素をヘリウムに変えて同じ事をします。
エントロピーはS からΔS増えます.。
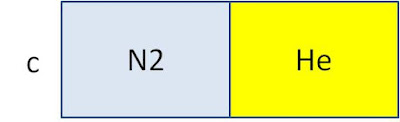
C
ギブスのパラドックスからCについて、次のことが言えます。
窒素とヘリウムの詰まった箱の壁に穴を開けるとエントロピーが大きくななり、そして増えたエントロピーは正確に2ΔSになります。
.
C のエントロピーはAとBの足し算と考えるのです。
穴を開ける前、穴を開けた後、CのエントロピーはAとBの足し算で計算できます。
(このことは、少し統計力学を勉強すればウソのように納得できます)
さて、ビジネスマンのいる部屋へ帰りましょう。
2.重力場でのエントロピー
今度は高さで圧力が変わる程、とてつもなく大きな部屋にします。
部屋は窒素とヘリウムで満たされ、熱平衡に達しています。
これは次のように表現できます。
部屋は窒素とヘリウムで満たされ、比エントロピーの値はどこでも同じになっている。
700hPaの高さで混合気体を風船に詰めます。
エントロピーを変えないように風船を圧縮します。圧縮するエネルギー源は位置エネルギーです。
乾燥断熱減率や乾燥断熱減率とエントロピーで議論したように、重力場での平衡状態では次の2つの関係がありました。
A:CpT+mgZ=Const
B: S(Z) =Const *S (Z) は比エントロピーです。.
A はエネルギー保存則です。
B は熱平衡を仮定した表現で、比エントロピーは何処でも同じになっていることを意味しています。
(実は、普通の温位の定義式はBを使っています。)
位置エネルギーを使って圧縮するとエンタルピーCpTが大きくなります。これは温度Tが上がることを意味します。
こうして風船を850hPaまで降ろした時、風船の中の窒素とヘリウムの分圧と温度は風船の外と同じでなければなりません。
なぜなら、もし、分圧か温度が外と違ったらBの関係がそもそも成り立ってれいなかった。
熱平衡ではなかったことになるからです。
700と850hPaに限らず、分圧比は何処でも同じでなければなりません。
高さZ= 0の圧力をP (0), 窒素とヘリウムの分圧を其々PN (0)、PH(0)としましょう。
P(0)は次のように書けます。
P(0)=PN(0)+PH(0)
P (Z)は乾燥断熱減率の議論から次のように書けます。
P(Z)=P(0)EXP-∫(mg/RT(Z´))dZ´ (2-1)
積分範囲は0からZです。
(乾燥断熱減率では平均温度を使っていますが、平均温度など使うべきではありません)
分圧比は高さによって変わりませんから次の関係があります。
PN(Z)/P(Z)=PN(0)/P(0)
PN(Z)=P(Z)PN(0)/P(0)
=P(0)EXP-∫(mg/RT(Z´))dZ´×PN(0)/P(0)
PH (Z) も同じです。
PH(Z)=PH(0)EXP-∫(mg/RT(Z´))dZ´ (2-2b)
(2-2a)と (2-2b)の物理的な意味は混合気体は勝手に分離しないと言うことです。
実際の大気でも、分圧比が何処でも同じなのは観測事実として知られています。
しかし、教科書では (2-2a)と(2-2b)は暗に成り立たないとされています。.
その説明は大体次のようなものです。
ヘリウムだけの大気を考えます。
例えば圧力が半分になる高さをHHとします。
次に窒素だけでできた大気を考えます。
圧力が半分になる高さをHNとします。
すると、次のようになります。
HH>HN
教科書はヘリウムの圧力が半分になる高さが窒素より高いからヘリウムが浮くのだと説明します。
しかし、これでは観測事実と一致しません。そこで、教科書は分圧比が一定になるのは“かき混ぜる力”が働くからだと説明します。
・・・・・・?
私は次のように反論します。
教科書は混合気体の静水圧平衡すら考えていない。
混合気体のヘリウムは混合気体の影響を受け、ヘリウムだけの影響をうけるわけではない。
それに、かき混ぜる力ってなんですか?
私には、ご都合主義の説明にしか思えません。
私はかつて、かき混ぜる力とは渦のことだと説明されたことがあります。
説明者は渦が無ければ、本当に混合気体は勝手に分離すると思っているようです。
しかし、この説明は渦が無ければエントロピーが減少すると言っているのと同じです。
こうして彼は放射冷却や温室効果を信じるようになります。
彼は間違っています。
3.H2 0 の高度分布.
次のグラフは2007/9/8 00z 館野の温位エマグラムです。
既に日射により、0mから750mの温位が同じ値になっています。
乾燥空気(水蒸気も含んでいますが・・)として等エントロピーになっていると言うことです。
750mの湿りをどのように考えるべきでしょうか?
私は経験的にこの高さの積雲が広がり始めていると考えます。
そして、この湿りは日射により分圧比が同じになったためと説明します。
大気中の水蒸気が理想気体のように振る舞った結果と考えられます。
この時の水蒸気は等エントロピーになって750mまで輸送されているのです。
そうだとすると水蒸気の分圧は (2-2a)から次のようになっているはずです。.
e(Z)=e(0)EXP-∫(mg/RT(Z´))dZ´ (3-1)
e(0)/P(0)=e(z)/P(z)=Constant (3-2)
次のグラフは P とeの分母、分子が逆ですが P/e.をプロットしたものです。
P (z)は気圧でe(z)は水蒸気圧です。.
P (z)は気圧でe(z)は水蒸気圧です。.
このグラフからは気圧と蒸気圧には何らかの規則性があると思いたくなります。
あなたが気象関係者なら、何故このようなグラフを今まで見たことがなかったのか、考えてみるべきだと思います。








0 件のコメント:
コメントを投稿