空気の不思議

気象にはウソや間違えが多いと思います放射冷却はウソの典型ですね気温は地上1.5mの高さで観測していますが地表面の温度は地上1.5mの湿球温度という温度になります放射冷却は放射対流モデルで温室効果の根拠にされるデタラメぶりです原発が絡んでいますね温室効果で原発がクリーンエネルギーに化ける温室効果で温暖化させているエネルギーを説明できるか？温暖化させているのは先進国の過剰なエネルギーですウソツキは誰だ

2011年10月26日水曜日

筑波山の湿球温度とは何？　　湿球温度と気温・露点の相関

１．湿球温度と気温・露点の相関
・・・申し訳ありませんが・・・少し数学をつかいます。・・・
偶然ですが、湿球（温度）と露点（温度）に強い相関があったことを「筑波山の湿球温度とその相関」で報告しました。
湿球は気温とも強い相関があります。

湿球は気圧、気温、露点（水蒸気圧）によって決まります。

CpT＋ｍｇZ+（E（Td）／P）×L＝CpTｗ＋ｍｇZ+（E（Tw）／P）×L　　(1)

Cp：定圧モル比熱　T:気温　m：空気1モルの質量　ｇ：重力定数　Z：高さ
E(Td)：蒸気圧（水蒸気の分圧）　Td:露点温度　Tw:湿球温度　P：気圧
L:1モルの水が水蒸気になるために必要なエネルギー

観測場所は筑波山頂で高さは一定です。
気圧Pは大きく変動しませんので、Pを一定とすると湿球温度Tｗは
Tw＝Tw(T,Td)
とかけます。
常識的に気温が露点＝水蒸気圧→水蒸気の量に影響を与えるとは考えられません。
こうした状況でTwがT及びTdとの相関係数が高いとは

Tw＝Tw(T,Td)＝aT　+　bTd　＋ｃ　(2)

になると言うことです。
aとbは(1)でTｄ＝Constとして
ｄTw/ｄT＝a
そして、T＝Const（＝b）として
ｄTw／ｄTｄ=b
で求められます。

（（１）からa、bを求めるのは難しくありませんが興味のある方はEをTwとTdでそれぞれ偏微分した値は違うことに注意して下さい。）

（2）の関係が実在空気に存在すると言うことです。

5月12時のデータを示します。

上のグラフ「5月12時　気温対露点」は、たて軸が気温T、よこ軸が露点Tdの生データです。
湿球（温度）Twは統計処理したら気温と露点を足して2で割ったような
Tw=0.45T+0.48Td+0.81
で近似されました。

ｙは生データの気温（＝X1）と露点（X２）で求めた湿球の予想です。
（切片Cは０かもしれませんが・・・一応残しておきました。）

低気圧や前線の通過等の変化がなければ、16時の湿球温度は翌朝の最低気温予想に利用できるかもしれません。
(湿球温度は全エネルギー、温度は乾燥空気のエネルギー、露点は水蒸気のエネルギーに関係し位置エネルギーは一定です。エネルギー保存則から温度を湿球温度と露点で予想ができそうです。気温予想は相対湿度を使っていると聞いたことがあります。統計的に相対湿度を使い気温予想するよりましかもしれません。）

2．地表温の日変化
さて、数学は終わりで俄田引水理論です。
筑波山シリーズを読んでくれた方はおわかりでしょうが・・・
地表温度は南中時刻を過ぎると冷え始め、夕方湿球温度付近に落ち着きます。

日照で加熱されているのに、加熱が弱まると冷え始めるのは「加熱（日照）」と同時に何らかの「冷却システム」が働いていると考えられます。
冷却システムがなければ、加熱されている間は地表温の昇温ペースにぶっても昇温し続けるはずだからです。
また、地表温の下降の原因が放射なら日照がなくなっても地表温は下がり続けるはずです。
「冷却システム」は湿球温度または湿球温度に関係する下限が存在しているようです。

冬は地表温のほうが*低なりますが夜間に湿球との相関が高いことは変わりません。

空気には地表面を湿球温度にしようとするメカニズムがありそうです。

*Lは水蒸気が液体の水になるとして計算している点に問題があるかもしれません。私の宿題にしておきます。

こうした現象や実在大気の＊温度減率を放射冷却や温室効果のような放射理論で説明するのは困難…と言うより間違えだと思います。
「放射冷却は冗談だ」と筑波山のデータが示しています。

＊実在大気の温度減率は相対湿度が100％に達していなければ乾燥断熱減率になるはずです。今の気象の理論では、曇りや晴れの日は乾燥断熱減率になるはずです。
？？1月グラフ注意？?それにしても、1月の7、8時は地表面がまだ気温より低いのに気温が上がり始めます。地表が1.5ｍの空気を暖めるのは不可能です。（湿球が上がり始めるのは理解できるが…）何が空気を暖めているのだろう？？？？地上1.5mの空気中に可視光を吸収する物質があるのかもしれません？
単純に空気を理想気体ととらえる悪習は止めるべきですね。空気の物性を研究すべきです。
余計な事が長くなりました。

3．相関が高い月低い月

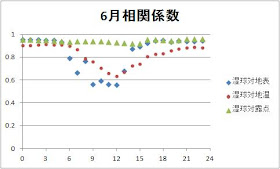
湿球対地表の相関係数が一番小さい5月と大きい9月を中心に見てみます。

3-1　5月の相関

5月は昼間の長い月です。

9時前の地表温変化が気になりますが・・（過渡現象かも？）

やはり南中時刻を過ぎると地表温は下がり始め、夕方湿球温度に落ち着きます。

湿球と地表の相関が一番高かったのは0.93（4時）、一番悪かったのは0.30(9時 )でした。
相関係数が低くなるのは地表温が上がる日中です。原因は日射による加熱と考えてよいでしょう。

次は5月4時の湿球対地表温のグラフで横軸が湿球で縦軸が地表温です。

湿球は気温と露点を足して２で割ったようなものですから気温と露点を加えて見ましょう。

気温と露点の境界は気温と露点が同じ温度で相対湿度100％の直線です。
ｙ＝ｘの直線の代わりに使えます。
この境界の上に分布する点は湿球より高く、下に分布する点は低いことになります。
地表温はこの境界近くの上下に分布していることがわかります。

次に地表温と相関の悪かった9時のグラフです。

相関係数は0.30ですからほとんど無相関に見えます。

　　
地表温は気温と露点の境界、湿度100％線の上に分布して湿球温より低くなりません。日照により加熱されているからだと思います。
1.5ｍの高さにはひょっとしたら湿球温度に近いオーブのような水粒が浮いているかもしれません。

見通しが10km以下の「もや」とは
微小な浮遊水滴や湿った微粒子により視程が１km以上、10km未満となっている状態。
だそうです。

12時には相関が少しよくなります。

確かに、湿球温が高いと地表温が高い傾向があるように見えます。
このあと相関係数は上がり続けますから、湿球温と地表温には弱い相関がでてきたと言えそうです。

再び相関が高くなった17時のグラフを見ます。

5月ですから、17時でも十分に日照はあると思いますが、湿球温度と地表温には0.90と強い相関が表れます。

地表温は湿球温度より低くなることはありますがほとんど地表温は湿球温より高くなっています。

18時になると、地表面は湿球温度が湿球温より低くなるケースが増えるようです。
18～19時に地表温≒湿球となり安定するようです。

3-2　9月の相関

5月に比べると変化は小さいのですが、やはり南中時刻を過ぎると地表温は下がり始め、夕方湿球温度に落ち着きます。
湿球と地表の相関が一番高かったのは0.97（3時）、一番悪かったのは0.70(11時 )でした。

3時の相関は

湿球－地表温の最大、最小、平均を見ると3.4℃、－3.0℃、0.05℃となりました。
相対湿度が気になるかもしれませんが、平均相対湿度は91.3％でいつも雲（霧）の中と言うわけではなさそうです。

11時

相関係数は0.70で湿球が高いと地表も高くなるような傾向は読み取れると思います。

傾いたサンドウィッチのような分布になりました。
湿球温と露点の相関は時間にかかわらず非常に高い値を示していますが、確かにこの時間も露点の分布も相関が高いことグラフからも推定されます。
この時間の露点と地表温の相関係数は0.53で湿球温と地表温の0.70より悪かったです。

　
9月は17時に地表温は湿球温度になって安定します。
17時の相対湿度の平均は90.0％でした。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
データは「筑波山気象・水文観測プロジェクト」からダウンロードしました。
筑波山気象・水文観測プロジェクトのホームページ
http://mtsukuba.suiri.tsukuba.ac.jp/
データがダウンロードできるページ
http://mtsukuba.suiri.tsukuba.ac.jp/sub6.html

機器構成
http://www.weather.co.jp/mtTsukuba/drawing/mtTsukuba_gif_2.gif

大昔、何かの読み物に
「永久に壊れない住宅の家賃は0円になる」
と書いてあったような気がします。
理論とは現実をよく映し出しますが、理屈はなんとなく納得しましたが・・・
やっぱり現実とは違うと面白く思った記憶があります。

放射性物質はいったい何年間管理しなければならないか私はしりませんが・・・
１千年、１万年、１０万年・・・もっと？（何かで読んだとおもうのですが・・何故しらないのだろう・・・・）
おそらく１千年ではないでしょう。
私の寿命から考えると数千年は永久と同じです。
放射性物質はどうも永久に管理しなければならないようです。
永久にコストがかかるわけです。
たぶん現実です。
発電コストの試算はインチキです。

2011年10月22日土曜日

筑波山の湿球温度とその相関

各相関係数を計算してみました。

要素は、湿球温（度）、地表温（度）、－１センチの地温（度）、露点（温度）です。

湿球温度について湿球温と露点の関係について温位エマグラムと湿球温度　―雨雪判別―

から再録しておきます。要素等はこちらを参照してください。

CpT＋ｍｇZ+（E（Td）／P）×L＝CpTｗ＋ｍｇZ+（E（Tw）／P）×L　　　（１）

CpTはエンタルピーと呼ばれるエネルギー

ｍｇZは水蒸気を含む空気の位置エネルギー

残りは水蒸気を液体にした時のエネルギーです。

乾燥断熱減率と温位エマグラムを参照してもらうと

Cpθe= CpT＋ｍｇZ+（E（Td）／P）×L

で（１）左辺は相当温位の中身であることが分かると思います。

気象で使う相当温位は、1000hPaの位置を基準（0メートル）としています。

おかげで、300hPaの相当温位予想の精度(安心して使ったのは強風帯の予想ぐらいだったかな？)が悪くなっています。

（理由：例えば850hPaの要素から計算して1000hPaの高度がちょうど地表面になったとしても300hPaの要素から1000hPaの高度を計算すると地中の深い所になり、この位置エネルギーの違いが誤差になっています。）

飽和相当温位と湿球温度の関係は下図のとおりです。

降水粒子が適当な大きさがあるなら、湿球温度が降水粒子の温度となります。

各気圧面の相当温位が分かれば、湿球温度は計算できます。

余計なことですが、これで雨雪判別ができます。

湿球　対　地表

　　　　MAX　　　　MIN　　　MEAN

01月　 0.93(03時) 　0.63(10時) 0.86

02月　 0.93(03時)　 0.47(11時) 0.85

03月　 0.95(06時)　 0.36(10時) 0.83

04月　 0.94(18時)　 0.45(10時) 0.83

05月　 0.93(04時) 　0.30(09時) 0.77

06月　 0.96(00時)　 0.56(12時) 0.84

07月　 0.93(20時)　 0.66(09時) 0.85

08月　 0.94(17時)　 0.69(10時) 0.88

09月　 0.97(03時)　 0.70(11時) 0.93

10月　 0.93(06時)　 0.54(10時) 0.87

11月　 0.94(04時)　 0.73(11時) 0.89

12月　 0.94(07時)　 0.67(11時) 0.89

湿球　対　－1センチ地温

　　　　MAX　　　MIN　　　MEAN

01月　 0.64(10時) 0.44(12時) 0.58

02月　 0.68(23時) 0.54(12時) 0.62

03月　 0.80(07時) 0.54(13時) 0.71

04月　 0.85(08時)　0.61(12時) 0.77

05月　 0.84(06時)　0.50(10時) 0.72

06月　 0.91(03時)　0.64(12時) 0.82

07月　 0.84(02時)　0.65(11時) 0.78

08月　 0.87(06時)　0.59(11時) 0.80

09月　 0.96(09時)　0.74(11時) 0.89

10月　 0.86(17時)　0.74(11時) 0.83

11月　 0.88(09時)　0.83( 04時) 0.86

12月　 0.85(09時) 0.76(14時) 0.82

湿球　対　露点

　　　　　MAX　　　MIN　　　MEAN

01月　 0.93(03時)　 0.75(14時) 0.88

02月　 0.93(07時)　 0.72(14時) 0.87

03月　 0.94(23時)　 0.76(14時) 0.89

04月　 0.91(00時)　 0.63(14時) 0.82

05月　 0.92(20時)　 0.77(13時) 0.87

06月　 0.96(22時)　 0.92(14時) 0.94

07月　 0.96(04時)　 0.95(21時) 0.96

08月　 0.97(09時)　 0.94(05時) 0.96

09月　 0.98(09時)　 0.96(13時) 0.97

10月　 0.96(08時)　 0.92(12時) 0.95

11月　 0.95(04時)　 0.85(14時) 0.91

12月　 0.95(01時)　 0.85(14時) 0.93

参考に9月のグラフを示します。

9月の相関係数

「湿球と地表」と「露点温度と地表温」の相関係数は全て

湿球と地表　＞　露点温度と地表温

となりました。

特に考えがあって、湿球（温度）と露点（温度）の相関を見たわけではないのですが・・・

かなり高い相関がありました。

湿球と気温にも相関がありそうです。（次回報告）

参考に気温と露点の2月の相関を示します。

黄色の線は相対湿度が100％になる線です。

とても、相関があるとは言えません。

次回は湿球温度が気温や露点温度と強い相関があったことを報告します。

確かに、気圧、気温、露点温度で湿球温度は決まるのですが・・・

データは「筑波山気象・水文観測プロジェクト」からダウンロードしました。
筑波山気象・水文観測プロジェクトのホームページ
http://mtsukuba.suiri.tsukuba.ac.jp/
データがダウンロードできるページ
http://mtsukuba.suiri.tsukuba.ac.jp/sub6.html

機器構成
http://www.weather.co.jp/mtTsukuba/drawing/mtTsukuba_gif_2.gif

気温は地表から　1.5メートル
地表温は地表
地温は地表から　マイナス1センチ
の温度です。